|
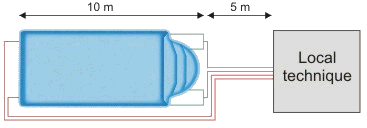
Analysons le circuit hydraulique,
en analogie avec un circuit électrique :
Nous avons un générateur (la pompe) et
deux types de récepteurs (le filtre et les canalisations).
La pompe fournit une pression qui
diminue en fonction du débit. Cette chute de
pression est due aux pertes dans l'impédance
Z (ou résistance) interne de la pompe. On peut
donc modéliser la pompe par un générateur
parfait fournissant Po (pression à débit
nul), en série avec une impédance interne
ZP de la pompe.
Le filtre
est équivalent à un autre générateur
en opposition avec la pompe, sa pression PF
sera de 0.5 bar quand il est propre, et 0.8 bar
quand il est sale (par construction, à vitesse
de 50 m/h). Cette contre-pression se déduira
de la pression de la pompe.
Les impédances
des canalisations ?
Les canalisations
aspiration et refoulement auront une impédance
ZA et ZR selon
leurs diamètres et leurs longueurs, calcul ci-après.
Dans le local technique, divers éléments
présentent un impédance à prendre
en compte : les canalisations elles-mêmes, mais
aussi les coudes, tés, vannes, etc ... La somme
de ces divers éléments constituera l'impédance
ZLT du local technique.
Connaissant
Po et ZP de la pompe, la contre-pression
PF du filtre et les impédances
des divers éléments, on pourra calculer
le débit d'eau dans le circuit hydraulique. |
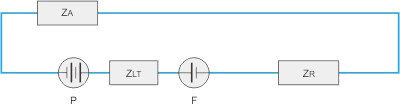
Eléments
du circuit hydraulique

Schéma
équivalent |



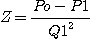


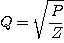 ou Q = (P/Z) 0.5
ou Q = (P/Z) 0.5